Simple Liner Regression 2

Hypothesis and Cost

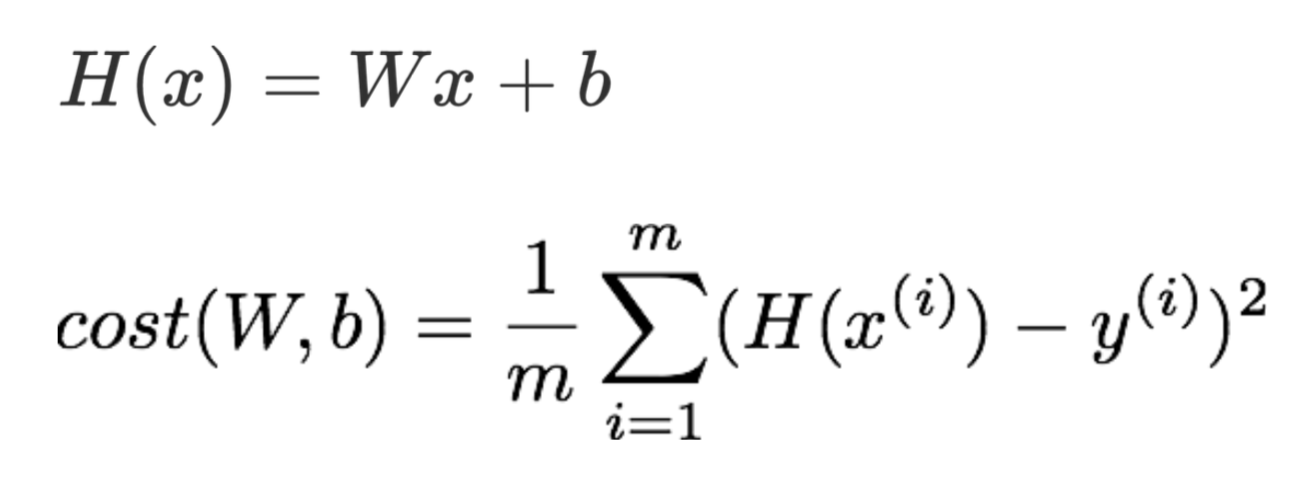
cost를 다시 생각해보자면,

y는 실제값입니다.

또한, 우리의 가설에서 실제값을 뺀 값을 에러라고 합니다.

이 에러를 제곱한 것의 평균을 cost라고 정의하고 있습니다.

위의 예제는 input 과 output이 같은 모델으로 우리가 w,b의 값이 1과 0이라는 사실을 알고 있습니다.

W, b를 구하기 위해 초기값을 임의의 값으로 지정해 줍니다.

이렇게 되면 우리의 가설을

hypothesis = W * x_data + b

이라고 정의할 수 있고, 이를 통해 비용은

cost = tf.reduce_mean(tf.square(hypothesis - y_data))

로 정의할 수 있습니다.

---

이제 cost에서의 함수를 자세히 알아보겠습니다.

• tf.reduce_mean()
  • reduce의 의미는 차원이 줄어드는 것으로 이 함수는 rank가 줄어들면서 mean을 구하는 것입니다.
• tf.square()
  • 제곱입니다. 에러의 제곱을 구하기 위해 사용합니다.

Gradient descent

• 경사 하강 알고리즘은 cost를 최소화하는 W, b를 찾는 알고리즘 입니다.

learning_rate를 먼저 설정해줍니다.

이 값은 계산시 얼마만큼 움직이며 계산을 할지 정하는 값입니다.

다음으로 이전에 구했던 가설과, cost의 정보를 tape에 저장해 줍니다.

W_grad, b_grad에 W,b 각각의 미분값을 저장해줍니다.

assign_sub() 함수는 자바에서 a -= b 와 같은 기능을 합니다.

지금까지의 과정이 한 번 학습을 한 과정입니다.

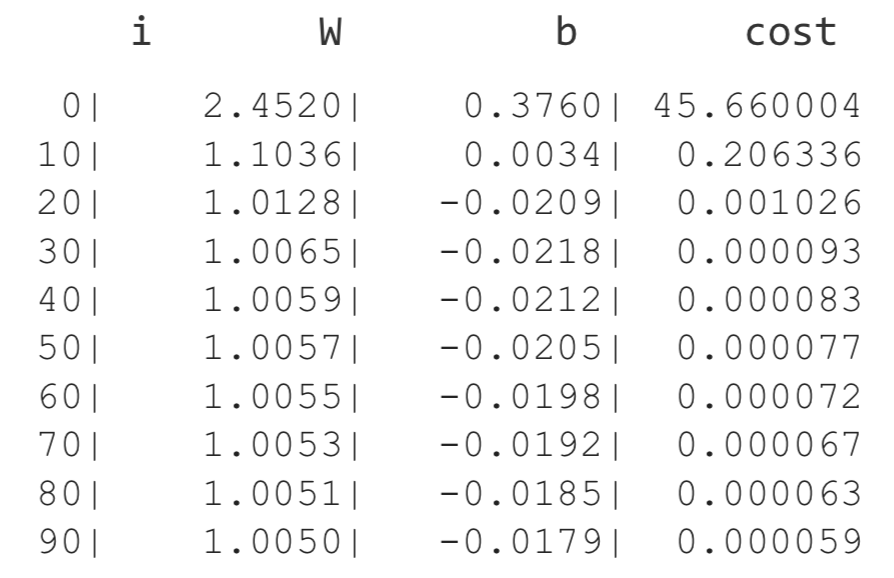
이 과정의 반복을 통해 W,b 의 값이 예상했던 값으로 수렴하고, cost 또한 감소하는 모습을 볼 수 있습니다.