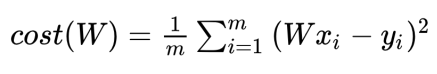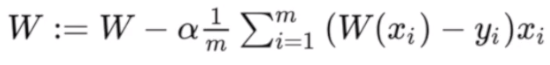Ml4

Cost minimalize

• Cost 함수를 파이썬과 텐서플로우 코드로 작성 해보겠습니다.

Cost Function in pure Python

import numpy as np

X = np.array([1,2,3])
Y = np.array([1,2,3])

def cost_func(W, X, Y):
    c = 0
    for i in range(len(X)):
        c += (W * X[i] - Y[i]) ** 2
    return c / len(X)

# W * X[i] - Y[i] : 오차
# 오차 제곱을 c에 누적해서
# 데이터의 갯수로 나누어줍니다. => 평균


for feed_W in np.linspace(-3, 5, num=15):
    curr_cost = cost_func(feed_W, X, Y)
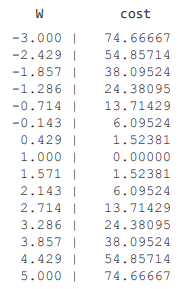
    print("{:6.3f} | {:10.5f}".format(feed_W, curr_cost))

# W값이 -3 에서 5까지 15개의 구간을 가집니다.
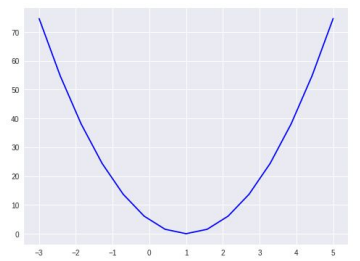
# cost는 W값에 의해서 바뀌는 모습을 출력합니다.
# 1.000에서 cost가 최소일 때를 찾을 수 있습니다.

Cost Function in TenserFlow

import numpy as np

X = np.array([1,2,3])
Y = np.array([1,2,3])

def cost_func(W, X, Y):
    hypothesis = X * W
    return tf.reduce_mean(tf.square(hypothesis - Y))

# hypothesis 에서 y를 뺀 값을 제곱하여 평균을 냅니다.

W_values = np.linspace(-3, 5, num=15)
cost_values = []

# 넘피의 linspace를 활용해서 -3에서 5까지의 구간을 15개로 쪼갭니다.
# 이 값을 리스트로 받습니다.

for feed_W in W_values:
    curr_cost = cost_func(feed_W, X, Y)
    cost_values.append(curr_cost)
    print("{:6.3f} | {:10.5f}".format(feed_W, curr_cost))

# 받은 리스트값을 하나씩 뽑아 W로 사용합니다.
# 이 W값에 따라 어떻게 cost값이 나오는지 확인합니다.

Gradient Descent

• gradient descent를 텐서플로우로 표현해 보겠습니다.
• gradient descent의 식은 다음과 같습니다.

alpha = 0.01
gradient = tf.reduce_mean(tf.multiply(tf.multiply(W, X) - Y, X))
descent = W - tf.multiply(alpha, gradient)
# descent가 새로운 W값입니다.

W.assign(descent)

• 위의 Gradient descent를 학습시켜봅니다.

tf.set_random_seed(0) 
# 코드를 다시 실행해도 동일하게 지연될 수 있도록
# 랜덤시드를 특정한 값으로 초기화 합니다.

x_data = [1., 2., 3., 4.]
y_data = [1., 3., 5., 7.]

W = tf.Variable(tf.random_normal([1], -100., 100.))
# 정규분포를 따르는 랜덤 넘버 [1] 개로 변수를 만들어서 W에 할당합니다.

for step in range(300):
    hypothesis = W * X
    cost = tf.reduce_mean(tf.square(hypothesis - Y))

    alpha = 0.01
    gradient = tf.reduce_mean(tf.multiply(tf.multiply(W, X) - Y, X))
    descent = W - tf.multiply(alpha, gradient)
    W.assign(descent)
    # gradient descent를 300번 진행합니다.

    if step % 10 == 0:
        print('{:5} | {:10.4f} | {:10.6f}'.format(
            step, cost.numpy(), W.numpy()[0]))

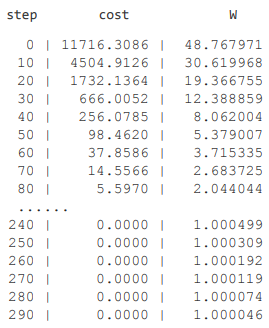
• cost의 값이 매우 큰 값이었다가 0으로 수렴합니다.
• W도 특정 값으로 수렴하는 모습을 볼 수 있습니다.
• W값에 상관없이 cost는 0, w는 특정한 값으로 수렴합니다.